Week 1: Decoding My Senior Project – An Introduction

Poonacha C. March 6, 2022 6:38 pm

Introduction – Current Objectives, Goals, and Plans:

● Hello everyone! Welcome to my first blog post! I am thrilled to have the opportunity of participating in a senior project! In my project, I hope to assist in making contributions toward the improvement of modern computing capability. In pursuit of our objective, we will develop a search algorithm, in the form of a 100 to 200-line Python program, that constructs digital representations of memristor-based nanoscale crossbar arrays to evaluate fixed-precision arithmetic expressions for both half-adders and full-adders. The memristor crossbar array, a potential solution to the Von Neumann bottleneck, is an emerging technology that can assist with memory processing. By applying flow-based in-memory computing methods, we will be able to evaluate arithmetic and Boolean expressions proficiently, which inherently improve time and energy expenditures by several orders of magnitude compared to traditional computing systems. We can evaluate the accuracy of our search algorithm by determining if they are able to successfully synthesize a crossbar that fits our defined constraints. Here, heuristics will be used to improve the algorithm’s performance. In addition to our Python program, we will produce a literature review on flow-based computing with an emphasis on how crossbar designs are synthesized from Boolean formulas. I will be interning under Dr. Sumit Kumar Jha, a Professor of Computer Science, and Mr. Suraj Singireddy, Dr. Jha’s Ph.D. student and research assistant, in correspondence with the University of Texas at San Antonio for a minimum of 15 hours a week.

Background – A Brief Insight into Von Neumann Architecture and In-Memory Computing:

● The Von Neumann computing model is a widely popular computer architecture that is built around the stored-program concept, a principle that allows instructions, programs, and data to be interchangeable, logically identical, and storable in a separate storage unit for memory. This allows computers to store applications, perform multiple tasks, and be reprogrammed more efficiently. As of today, von Neumann architecture continues to serve as the predominant foundation in quite a majority of modern-day computers; however, this very design poses a fundamental limitation. In the Von Neumann model, both the control and memory units are separated, which leads to restricted computing performance. Lower computing performance is a result of a computer’s memory wall, the rate at which data is fetched and shuttled from the memory unit to the processor and back for processing and storage. In-memory computing, a promising and revolutionary computing paradigm, seeks to resolve this issue as the approach allows for memory retrieval, storage, and processing to occur in the same unit. In other words, the memory and control units of the computer are not separated. Methods for developing a hardware structure for in-memory computing to take place have been organized in the past. An example is flow-based computing, an effective way of performing in-memory computing using sneak paths in nanoscale crossbar arrays.

I’m looking forward to moving on with my project! Check my upcoming blog posts for more updates!

Week 2: Preparation for Background Research

Poonacha C. March 20, 2022 6:57 pm

Hello everyone! I’d like to start off this blog post by detailing the steps I took in preparation for the upcoming weeks of my project.

Since my project assumes a high-level but extensive understanding of graduate-level, pre-requisite Computer Science content, I spent this week gathering and organizing as many research papers as necessary. The plethora of knowledge that I obtain from this array of literature will provide me with a solid academic background and a place of reference in case I need assistance during the development process of both the literature review and algorithm. Many of these sources, although only somewhat relevant to our topic of inquiry, were IEEE (Institute of Electrical and Electronics Engineers) and IEEE Spectrum abstracts and papers that I was given to draft my project proposal earlier in the year while others are ones I discovered from textbook PDFs and Google Scholar searches. I organized each paper into three distinct folders for topics concerning flow-based computing, memristors, and miscellaneous concepts. I expect to find and use more papers in the upcoming week. Later, I decided to review the fundamentals of the Python programming language by completing certain parts of DataCamp’s “Introduction to Python” course and referring to online Python documentation. I also went over the AP Research guidelines for literature reviews which will help me format my outline in later weeks. So far, my current weekly 15-hour schedule consists of working from 9:00 AM to 1:00 PM on Mondays and Wednesdays and 9:00 AM to 4:00 PM on Tuesdays although this is bound to change as we progress towards drafting and implementation.

I’ll see you next week!

Week 3: Continuing Background Research

Poonacha C. March 27, 2022 8:16 pm

Hello everyone, and welcome back to my blog!  I followed the same 15-hour schedule as last week (9:00 AM to 1:00 PM on Mondays/Wednesdays and 9:00 AM to 4:00 PM on Tuesdays), where I continued my research of important computing concepts in preparation for future activities and my personal understanding.

Continuing Background Reading:

● From Monday through Wednesday, I spent a significant amount of time thoroughly understanding how Boolean logic, Boolean Algebra, and Binary arithmetic work. I also covered the 7 different types of logic gates (AND, OR, XOR, NOT, NAND, NOR, and XNOR ), devices based on Boolean algebra, which are known as the basic building blocks of digital circuits. Watching YouTube videos that explain one-bit adders, full adders, and half-adders was an activity I engaged in to further my knowledge of combinational circuitry. In addition, I also began covering the structures and functions of memristors and crossbar architectures by reading a fascinating IEEE Spectrum article recommended by Dr. Jha titled “How We Found The Missing Memristor”.

Meeting Virtually with My On-Site Advisors:

● On Friday, I was able to meet with my on-site advisors via a Zoom meeting call for an hour. We spent the majority of the time discussing our future project goals and how we would tackle the remaining work left. It is important to note that the entire research process of writing up our literature review and final paper as well as programming will occur online, through Zoom meetings. Topics they advised me to spend a little bit of time on were search algorithms, matrix multiplication, and heuristics.

Week 4: Finishing Up the Literature Review

Poonacha C. April 4, 2022 10:11 am

Hey everyone, and welcome to this week’s blog! In this blog post, I will be covering the steps I took throughout the week to finish up our draft of the literature review.

Weekend – Prior to Week 4 (3/26/2022 to 3/27/2022): In a separate google document, I grouped all of the information I collected from IEEE and IEEE spectrum research papers into 4 categories: “Flow-based Computing and Its Applications“, “Memristors“, “Models of Memristor Crossbar Arrays“, and “How Crossbar Arrays Can Be Exploited for Faster Computation“. After deciding which sources I would use, I used a citation machine application called Zotero to create my works cited page in APA format for review ahead of time. From there, I decided that the subheadings of my body paragraphs in my literature review would be “Exploring the Possibilities of Boolean”, “Memristors and Crossbars”, and “Introducing Flow-based Computing” as these represent 3 main subsections that circumvent the academic literature required to explore our topic of inquiry.

Monday (3/28/2022): Once my outline of the literature review was approved, I dove right into writing up my first body paragraph which heavily centers on the topic of Booleans. Before doing so, I read a helpful GeeksforGeeks article titled “Introduction to Boolean Logic”, which served as my source for this subsection. First, I included a brief statement describing the background history behind “Boolean Logic”, including both its inventor and the previous propositional logic system that it derives from. Afterward, I briefly defined the following terms and concepts in order at an elementary level: “Boolean Algebra”, “Boolean Expressions”, “Boolean Variables”, “Boolean Values”, and “Truth Tables”. Below is the link to the article. Feel free to check it out whenever you can! https://www.geeksforgeeks.org/introduction-to-boolean-logic/

Tuesday (3/29/2022): When drafting the second paragraph, I wanted to introduce the rudimentary principles behind memristors and crossbars from my previous research last week. First, I described when, where, and how the “memristor”, the fourth fundamental circuit element, was discovered, and I researched a little about the etymology behind the two-terminal device. I also took the time to mention other circuit elements such as inductors, capacitors, and resistors to provide more background context. Finally, further elaboration regarding how memristors actually function, the importance of the “memristive switch”, the structure of “crossbars” and “crossbar architecture”, and “memristor-based nanoscale crossbar arrays” were provided.

Wednesday (3/30/2022): On Wednesday, my goal was to finish up my third and final body paragraph on flow-based computing. Here, I decided to deviate from my conventional approach of including definitions and explanations for every essential keyword. Instead, I introduced a problem and discussed how a proposed solution connects with a process that is important to the overall theme of our literature review. I began by emphasizing a complication in crossbar array architecture referred to as “sneak paths”, and I went on to highlight certain solutions called “sneak path constraints”. Following this, I clarified that such constraints were actually unnecessary and demonstrated how these sneak paths can actually be exploited to allow for in-memory computing to take place in a process called “flow-based computing”.

Thursday and Friday (3/31/2022 to 4/1/2022): Our approach to the literature review involves addressing a larger, more general topic and then using high-level summarization to narrow down our scope and establish a gap in published research we intend to explore. As a result, for our introduction paragraph, I initially wrote about the inefficiencies of Von Neumann computing architecture that result from a modern-day computer’s memory wall. Then, I went on to display how in-memory computing is much more efficient and can be applied practically through flow-based computing. From here, our topic of inquiry begins to narrow down, specifically to the tedious process of synthesizing nanoscale crossbars from boolean formulas for arbitrary program evaluation. The “gap” in existing publications is the lack of an efficient method of synthesis as other explored methods are usually implemented by hand. In my drafted conclusion, I included a detailed description of our new contribution, an automated process of synthesis, to bridge this gap as well as the limitations/drawbacks of our solution.

I plan to submit this draft to my on-site advisors for review, and once their edits are made, I will finalize in-text citations and the appropriate formatting in the following week. Once that gets done, I will be able to link a PDF version of this mini-paper to my next blog post for everyone to view and/or download. In addition, I recognize that throughout my blog, I have brought up a multitude of computer science topics that some of my readers cannot grasp immediately. As a result, in the upcoming blog, I intend to thoroughly go through any terminology in great detail while tying it to the overall purpose of my literature review and senior project goal. See you next week!

Week 5: Final Touches and Upcoming Developments

Poonacha C. April 10, 2022 6:59 pm

Hello everyone, and welcome back to my blog!

This week, my site advisors and I completely finished revising, editing, and finalizing the literature review! Again, the purpose of the review is to analyze the relevant academic literature surrounding our solution to our central problem, the lack of an efficient method of automating the synthesis of nanoscale crossbars.

In this post, I will do the following:

● a). Introduce future developments in our project.

● b). Provide a fully completed copy of my approved literature review accompanied by its finalized, corresponding outline.

● c). Highlight and connect concepts/terminologies that are relevant to my literature review and overall project goals.

Updates:

● Next week we will look at our Python algorithm for crossbar synthesis and hopefully begin implementation. A possible additional product for my project may be a research paper to summarize relevant information, methods of experimentation, and findings.

Finalized Outline for Literature Review:

● 1). Introduction:

○ a). Highlight the inefficiencies of the von Neumann computing model.

○ b). Show how the in-memory computing paradigm resolves the von Neumann bottleneck and briefly articulate how previous methods of applying in-memory computing principles have been implemented.

○ c). State the purpose of our literature review.

● 2). 1st Body Paragraph: “Exploring the Possibilities of Boolean”

○ a). Briefly define the following terms and concepts: Boolean logic, Boolean expressions, Binary values, Boolean expression values, Boolean operators, and truth tables.

○ b). Examples for Boolean values should be limited to “True” and “False” or “1” or “0”.

● 3). 2nd Body Paragraph: “Memristors and Crossbars”

○ a). Explain what a memristor is, and provide some information on its etymology.

○ b). Clarify how memristors function.

○ c). Describe what crossbars are, a crossbar’s designs, and the structure of crossbar architecture.

○ d). Include a concluding statement mentioning how crossbar designs and memristive technologies combine to form memristor-based nanoscale crossbar arrays.

● 4). 3rd Body Paragraph: “Introducing Flow-based Computing”

○ a). Introduce the problem of sneak paths and sneak path constraints (sneak paths’ proposed solution)

○ b). Establish the concept of flow-based computing at an introductory level.

○ c). Demonstrate how flow-based computing can be used to evaluate Boolean values.

● 5). Conclusion:

○ a). Bridge the gap that we brought up in the introduction,

○ b). Write up a description of our solution which is an algorithm that synthesizes memristor-based nanoscale crossbar arrays to perform fixed-precision arithmetic using flow-based in-memory computing

■ i). Discuss how the algorithm works, emphasize the importance of heuristics to optimize its efficiency, and mention that our crossbar designs are synthesized virtually.

○ b). Highlight the limitations of our solution we have or mention any drawbacks of our solution.

● 6). Sourcing/Formatting:

○ a). The works cited page will be in APA format.

Here is a copy of the paper: Literature Review

In the previous blog post, I mentioned that I would clarify confusing concepts for your understanding. Below, I have attached a flowchart that connects everything important to our overall project goals.

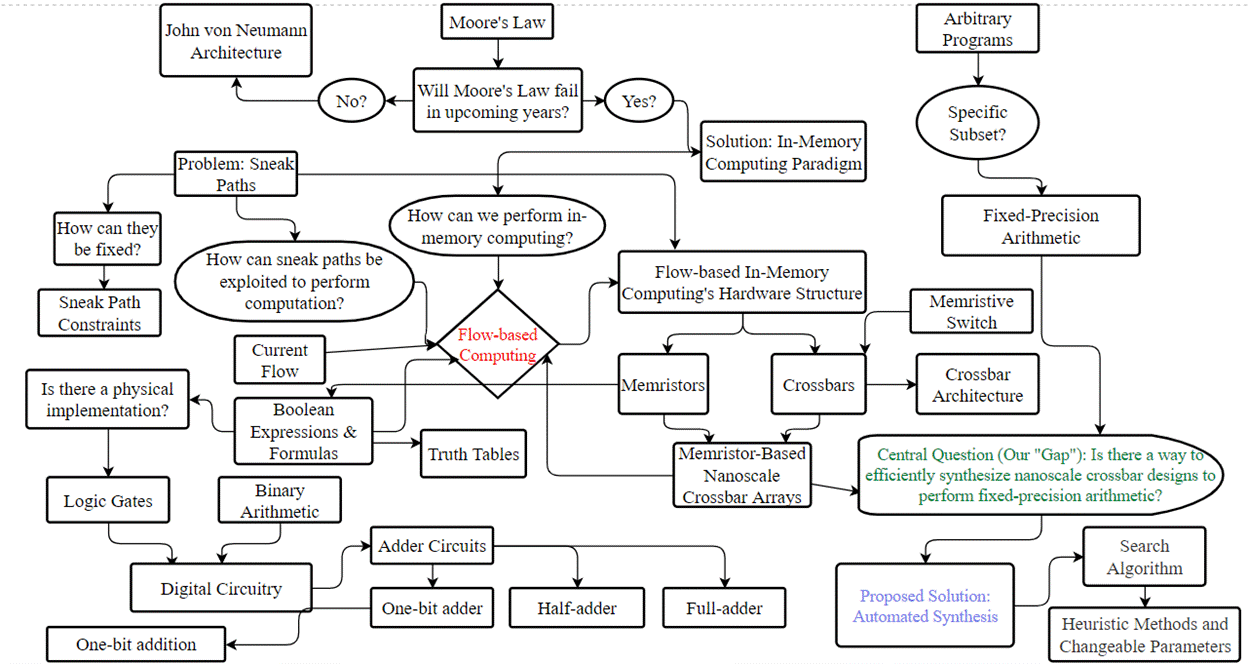
Week 6: Overview of Our Synthesis Algorithm

Poonacha C. April 17, 2022 7:00 pm

Hello everyone, and welcome back to my blog! During the 6th week of my project, I primarily focused on understanding our base Python algorithm created by my site advisor, Mr. Suraj Singireddy, which helps synthesize nanoscale crossbar designs to perform fixed precision arithmetic using flow-based computing. Our synthesis algorithm can be broken down into three main parts: 1). Generating a random crossbar design under a set of search parameter constraints and heuristics, 2). Checking if our design is equivalent to our target Boolean expression. 3). Executing important methods in our main loop and displaying various results in a human-readable format. This algorithm was created using a “Google Colabatory (Colab) notebook”, a product from Google research that allows us to write executable, arbitrary Python code through a web browser and share it easily with others. Another important detail to note is that our synthesis algorithm is limited to one Boolean expression and type of adder circuit only; it cannot print out crossbar designs for multiple Boolean expressions and circuits at the same time. For example, this week’s Python program works only for a half adder and the Boolean expression, “x1 & x2”. If we wanted to execute this program for a full adder instead with the same or different Boolean formula, we would have to change the dimensions of our crossbar design as well as other search parameters, heuristics, and parts of our code, a process which we will further continue to explore in the coming weeks. Below, I have snipped different parts of our source code in order and provided several explanations of it for your understanding.

Part 1 – Import Statements:

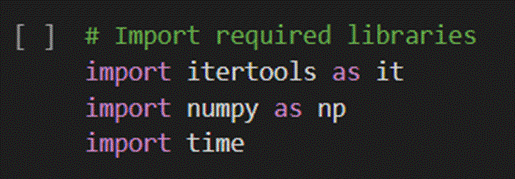
The first part of our synthesis algorithm and any Python program is to import Python libraries, collections of modules that contain bundles of reusable code. This allows the programmer to simplify their work since they don’t need to re-write the same code, and it enables us to use special functions and commands to accomplish complicated tasks. We import the “itertools” module so that we can primarily gain access to the “itertools.product()” function to help find the cartesian coordinate from a given iterator. The “as it” segment of the code allows us to reference this module in the form of “it.function()” since it can be quite tedious to type our “itertools.function()” multiple times.  The “NumPy” library enables us to create “NumPy” arrays and perform several high-level mathematical functions and operations on them which we can refer to as “np.function()”. Finally, the “time” module will provide us with the means to measure the runtime of our algorithm later on in the program.

Part 2 – Search and Heuristic Parameters:

Before we dive into the random search function, we have to set a few parameters for crossbar selection and generation. These parameters serve as constraints to ensure that we only select crossbar designs that match our desired specifications. Since this algorithm is guided for a half-adder, we create a NumPy array to hold every desired output for each input configuration of our target Boolean expression. In essence, the truth table for the Boolean expression, “x1 & x2”, is assigned to a variable we define as “target_tt”. Then, we specify that our crossbar design must have 3 rows and 2 columns while also mentioning that there are only 2 variables within the expression we’ve chosen. It has also been decided that our output nanowire must be located on the 1st row and the end of the 2nd column. Our heuristic parameters assist in improving the performance of the random search in “Part 3”. Here, we have set the density, the probability of how often a memristor in a crossbar is assigned to some variable, to 0.8. This means that for every memristor in the crossbar, approximately, 80% of them have been set to 1, which signifies low resistance, allowing free current flow through these memristors. The minimum and maximum frequency, denoted by “min_frq” and “max_frq” represent the minimum and maximum proportion of memristors assigned to each variable, x1 & x2. Therefore, a minimum of 0 memristors must be assigned to x1, and that minimum amount should be assigned to x2 respectively as well. From the last line of code, we can determine that approximately 50% of our memristors should be assigned to a negated variable, ~x1 or ~x2 (not x1 or not x2).

Part 3 – Random Search:

Above, you can find our heuristically guided search algorithm which will generate a random crossbar design subject to the constraints provided in Part 2. There have been comments included within the image to show which segments of the code correspond to how some memristors in the crossbar are randomly set to “0” or “off” (signifying high resistance and preventing current flow), the process by which variables that fit within frequency boundaries are located, and how some variables will be randomly negated. Once these verifications have been made, the random search section proceeds to return a matching design in the form of a “R x C” (Row by Column) matrix where each D[i, j] entry can be associated with the memristor at row i and column j. Furthermore, the possible assignments for memristors can be the following: always on, always off, associated with some Boolean variable, or associated with some negated variable.

Part 4 – Equivalence Checking:

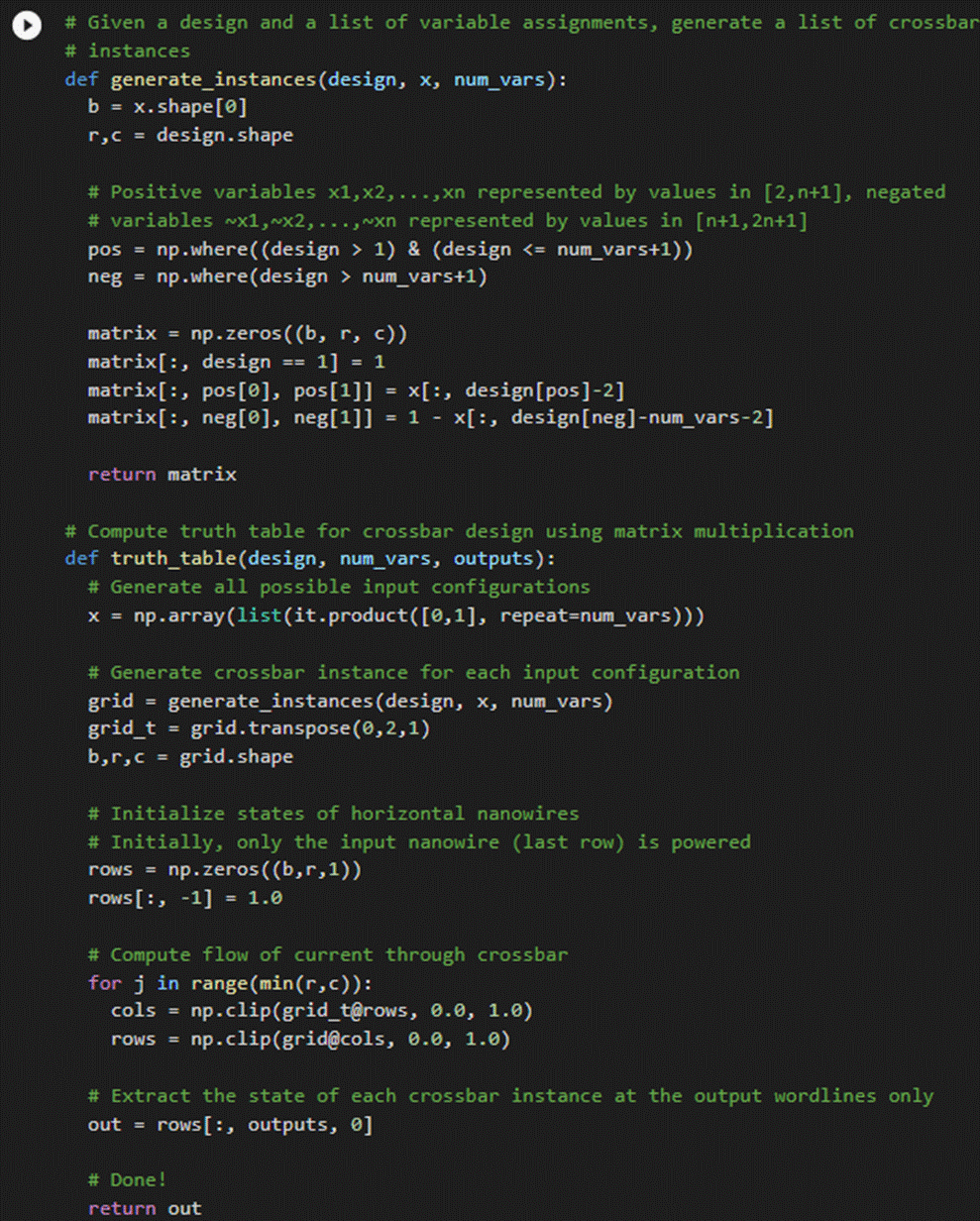
However, further verification is necessary to display accurate designs. This is where equivalence checking comes into place. After constructing a possible, functional crossbar that obeys our limitations, equivalence checking will verify if the output of our design produced by flow-based computing is equivalent to the output of our target boolean expression. Since this block of code is probably the most complex piece of the puzzle, our simulation of flow-based computing can be summarized in these 3 steps:

● a). The program will generate all possible input configurations of our target Boolean formula in the form of a 2D array, [[0,0], [0, 1], [1, 0], [1, 1]].

● b). A crossbar “instance”, a design with all associated values (of each variable occurrence) mapped onto crossbars, for each input configuration will be generated in the form of a matrix M of zeros and ones.

● c). A passing flow of current through the crossbar instance at the bottom-most wordline will be repeatedly simulated until our design’s output is determined.

Part 5 – Helper Function:

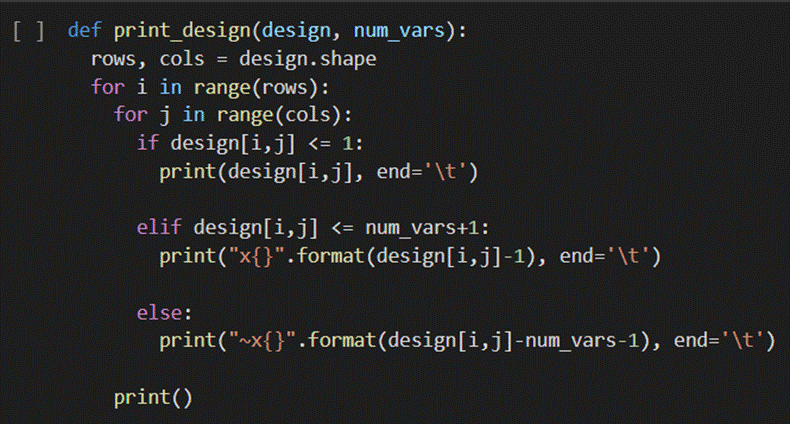
Once we have confirmed that our verified crossbar design matches our target Boolean expression through equivalence, we can proceed to digitally display our design by printing it out in a readable format using a helper function.

Part 6 – Main Loop:

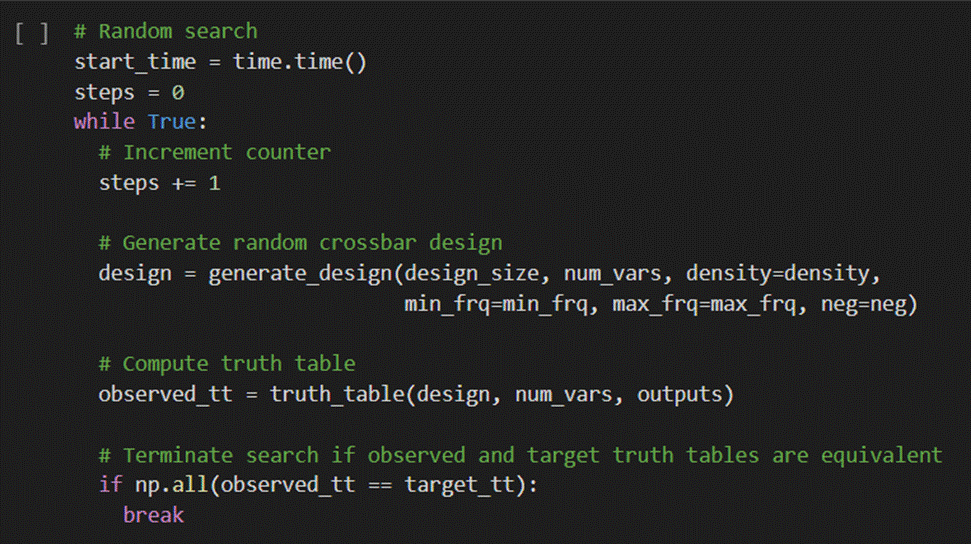
Here, we use the time function to start Python’s digital timer once the main loop starts to run, and we call our previous functions in while loop, an infinite loop that will only terminate once our random design has been generated, its truth table has been computed, and if the design’s truth table matches the target truth table.

Part 7 – Results:

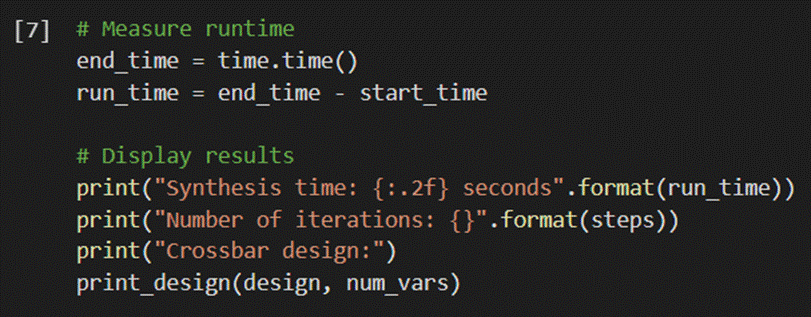
The code above stops the Python timer, giving us the end time of the algorithm. We can calculate the run time of our algorithm by subtracting our starting time from our end time. All results will finally be displayed here, including the number of iterations required to find a matching design.

Hopefully, you now have a clear picture of the steps our program takes to achieve our goal. Next week, we will look at and analyze some of our output designs in greater detail, so the process of flow-based computing on the crossbar can be better visualized. In addition, we plan to make some changes to our algorithm going forward in order to carry out the implementation process for a full adder or other expressions. See you then!

Week 7: Optimizing Our Algorithm for Full-Adder Circuits

Poonacha C. April 24, 2022 6:59 pm

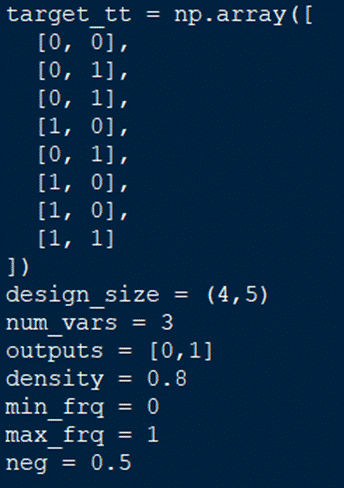
Hey everyone! Last week, I provided a step-by-step conceptual breakdown of our crossbar synthesis algorithm that specifically assumed the conditions of a half-adder circuit. This week, you will be able to see some of the changes we made to our Python program’s “Search and Heuristic Parameters” section, which helped us optimize algorithmic implementation for full-adder circuits instead! Although the initial version of the algorithm and our new one didn’t differ as much as I thought, it was necessary to spend quite a bit of time first figuring out what the original code lacked for accomplishing our new goal. Since a full-adder circuit’s truth table contains twice the number of input configurations than that of a half-adder and 3 different variables (X1, X2, Cin where Cin represents the “carry input”) within our chosen Boolean formula (X1 AND X2 AND Cin), we concluded that we have to modify the values of our “target_tt” NumPy array. Instead of assigning only 4 lists to “target_tt”, a total of 8 lists are required to represent all of the output configurations which are equivalent to the Binary sum of all of your inputs. Possible Binary sum values include 0, 1, 2, and 3 . Each list contains 2 numerical values, the “carry out (referred to as Cout)” and the “sum ( referred to as S)” and when put together, you get that particular binary sum value for each set of those 3 input values. As a result of this, we also changed “num_vars” from 2 to 3. After referencing another research paper, we determined that our crossbar should contain a minimum of 4 rows and 5 columns, so we set “design_size” to (4, 5) Below, you will see an image that displays our revised section of Python code.

One problem we do have with our program code is that our digital crossbar designs are taking too long to show up on the output window. We know that there is no problem with the accuracy of our algorithm, otherwise, a syntax error would have popped up. While an incredibly large synthesis time was anticipated for the full-adder, we tried to resolve the issue by executing the Python script on the classic Python IDLE shell. However, after hours of compiling and running our code, our designs cannot be displayed as a result of thousands of iterations from truth table checking. Right now, we don’t expect the time duration to reduce, but we hope to bypass this issue next week. See you then!

Week 8: More Updates and Our Approach for Experimentation!

Poonacha C. May 1, 2022 6:59 pm

Welcome back! Last week, we looked at some of the changes we made to our optimized synthesis algorithm’s code for the classic full-adder circuit truth table. Although accurate, we still had to overcome our problem with the Python program, an incredibly long run-time responsible for crossbar design output delay. Nevertheless, we spent a good amount of time this week trying to come up with realistic solutions in an effort to obtain our 4-by-5 crossbar; my site advisors and I even tried to let Python IDLE run for a long period time, even leaving our computers on for a total of 1 to 2 days at a stretch. Unfortunately, we were still unable to see our digitally synthesized designs as a result of delays in iterations and truth table checking, however, we do have some results from our initial program which produces designs assuming the conditions of a half-adder circuit instead. Check them out below!

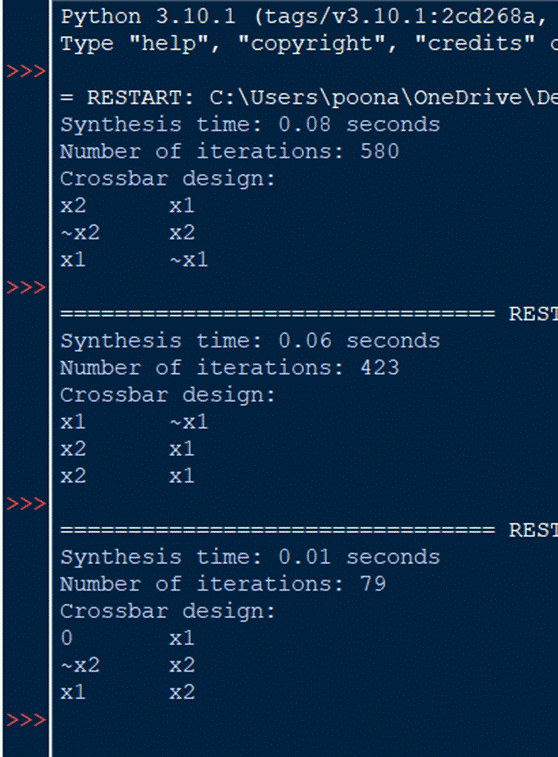
For each of the 3 outputs in the image above, you can see that the program not only constructs a 2-by-3 matrix of memristors with their randomly assigned Boolean and negated variables but also keeps track of the number of iterations and the total time required for the program to finally find a matching design and terminate out of the while-loop. Going forward, next week, we plan to start conducting trials to further explore the capabilities of our algorithms by varying the values of the parameters of the half-adder algorithm and assessing its correlation with the runtime. Afterward, we will also try to find a certain configuration of parameters that minimizes the synthesis time as much as possible.

Week 9: Progress on Data Collection

Poonacha C. May 8, 2022 7:00 pm

Hi everyone! Welcome back to my blog!

This week we finally began conducting trials with our half-adder synthesis algorithm. In the previous post, I stated that the intended purpose of experimentation was to configure our parameters in such a way that our Python program will generate accurate crossbar designs within the smallest synthesis time possible. Believe it or not, we were able to get a final synthesis time of 0.00 seconds! While the program doesn’t actually take zero seconds to produce an output, the Python IDLE Shell rounds off any synthesis time value to 2 decimal places only, which tells us that our designs were constructed in an incredibly short amount of time. Let’s go through our methods of data collection! Before starting, we first checked if the output configurations of the half-adder truth table were correct as different values for this parameter can cause a drastic difference in the number of iterations required for the process of truth table checking of randomly selected nanoscale crossbar arrays. It’s important to emphasize this because initially, one of our output configurations was incorrect, so even though we determined the optimal values for heuristic parameters, our designs wouldn’t have been ideal for a half-adder circuit forcing us to start over again. Afterward, we began varying the dimensions of our crossbar (# of rows & columns) by altering and setting the design size variable until the synthesis time crossed over 2 minutes. A thorough level of examination and verification is required, so we decided that a total of 10 trials would be necessary to determine the average synthesis time of one particular design. Despite this, values within the same data set sometimes drastically differed from each other. As a result, we repeated this process, but instead of noting down the time values, we made sure to conduct 10 more separate trials for each design which contain a data set for the number of iterations the program ran through until terminating. Here is the list of selected design sizes: (3×2), (3×3), (3×4), (4×3), (4×4), (4×5), (5×4), (5×5), (5×6), (6×5), (6×6), (6×7). After determining which dimensions out of our list produced the smallest average time and number of iterations, we began to vary the crossbar density, the parameter for negated variables, and a range of minimum and maximum frequencies. using the same method highlighted above (recording and calculating the averages for synthesis time and iteration values). Our data was collected using Microsoft Excel, where we also generated relevant graphs and figures to represent trends and optimal values for future analysis.

Next week, we will finish up our presentation an final paper.

Week 10: Preparing My Presentation and Final Product

Poonacha C. May 15, 2022 7:01 pm

Hey everyone! Welcome to the 10th and final blog post!

I spent the majority of this week working on the PowerPoint presentation for the Senior Project fair next Saturday. Most of my time outside of my daily zoom meetings with my site advisors was dedicated to organizing the required content on a separate outline. In the previous week, I already finished drafting the first couple of slides which contained a simplified version of my “research question” and the pre-requisite “background information” necessary to understand the purpose of investigation in my project. Since my topic of inquiry assumes a thorough understanding of several advanced concepts, it took me a while to finalize the exact order of computer science engineering principles I wanted to introduce on each of my “background research” slides. Afterward, I focused on summarizing my research process for the past 9 weeks while also comparing and contrasting my blog posts to the initial methodology I proposed in my Senior Project syllabus. Since presenting results and findings is an integral part of our PowerPoint presentations, I organized my synthesis time values from my experiments (for half-adder algorithmic optimization) into tables and graphs on another Excel spreadsheet. From there, I conducted a thorough analysis of our collected data, drew conclusions, and finished up the remainder of the slides left. Helpful images, diagrams, and figures were added throughout to improve context. On Friday, I gave a brief overview of my presentation in front of Dr. Jha and Mr. Singireddy during a 30-minute virtual meeting. Finally, we improved the format of our Google Collab workspace which contains our search algorithm, a Python program (and final product) with adjustable and optimal parameters for half-adder and full-adder circuits.

The content is a (hopefully) more permanent copy of the BASIS Charter School blog hosted here: https://basisedtx.com/san-antonio-shavano/senior-projects/week-2-preparation-for-background-research/